Transformer XL

Paper link : https://arxiv.org/abs/1901.02860, ACL 2019

Introduction

Language Model 은 long-term dependency가 요구되는 Task.

기존에는 RNN + Attention Mechanism 을 사용하여, Sequential data를 처리를 하였지만, RNN은 gradient vanishing and explosion에 관한 문제점이 존재함. gradient clipping의 기술을 써서 해결을 하지만, 충분치 않을 수 있음.

또한, LSTM 계열은 이전 연구들에서 약 200개의 context words를 평균적으로 사용한다고 알려져 있음. Attention mechanism은 이러한 제한된 dependency를 해결하는 기술로 사용되어짐.

트랜스포머(Transformer)는 2017년에 구글이 발표한 논문인 “Attention is all you need”에서 발표가 되었고 Attention만으로 Encoder와 Decoder를 구현한 모델, Transformer의 Encoder는 다양한 task에서 SOTA를 달성했던 BERT의 모듈로 사용됨.

하지만 Transformer 모델은 고정된 길이의 Segment를 가지고 있고, 사전에 정의된 컨텍스트 길이를 초과해서 Attention이 불가능한 단점이 존재.

Transformer-xl는 이러한 문제를 해결하기 위해서 Segment Recurrence를 제안하고, 기존 위치에 적대적인 값을 가지는 Absolute Positional Encoding의 문제를 해결하기 위해 Relative Positional Encoding을 도입.

최종적으로 RNN 대비 80%, Transformer 대비 450% 긴, 기존 Transformer 보다 긴 long-term dependency를 해결하였으며, Article Generation으로 수천 단어 정도의 term 생성이 가능해짐.

Model

Vanilla Transformer Language Models

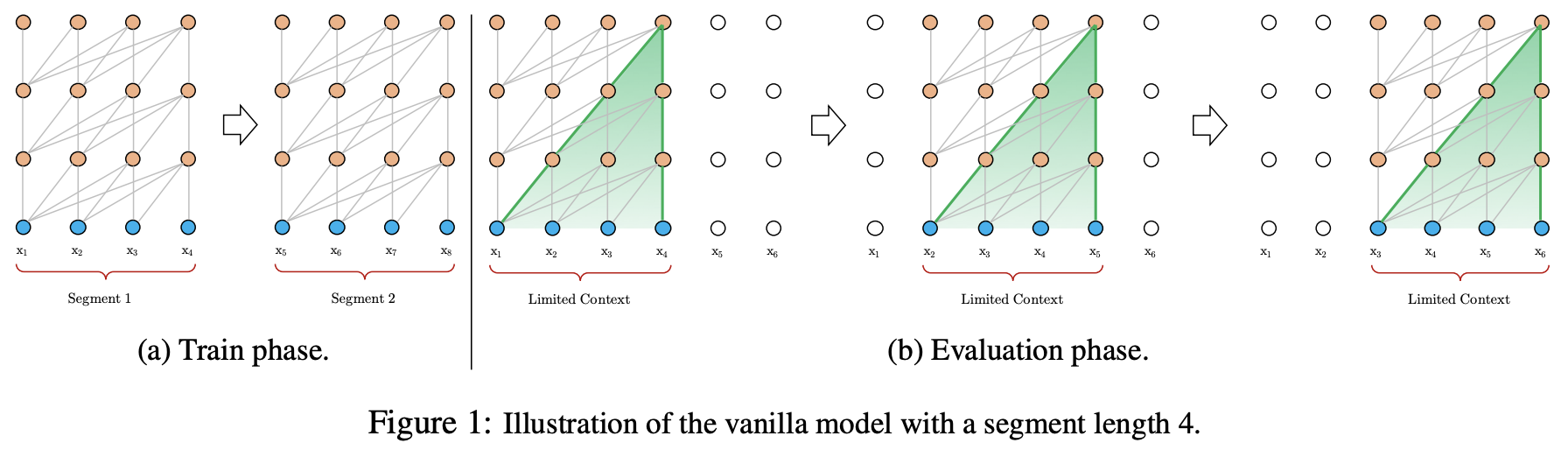
Transformer 또는 self-attention을 LM(Lauguage Model)에 적용하기 위한 핵심은 어떻게 임의의 긴 context를 고정된 길의의 representation으로 학습하는 것임.

무한한 memory와 계산이 가능하다면, 전체의 context sequence를 feed-forward neural network와 비슷한 uncoditional Transformer decoder를 사용하여 처리하는 방법이 가장 심플함.

현실적으로 가능한 approximation은 전체의 corpus를 나누어 segment를 만들어 사용하는 것.

Transformer는 정해진 길이의 segment로 corpus를 나누어 학습을 하는 구조로 이루어져 있음.

Vanilla Transformer 는 고정된 길이의 Segments 단위로 나누어져, 사전 정의된 컨텍스트 길이를 초과하는 장기 의존성을 캡처할 수 없는 fixed-length context 문제가 발생됨.

또한, 고정된 segment 길이 이상의 문장을 처리하기위해 segment1과 segment2로 나누어 처리를 하게 되고, segment에 따라 연관성이 쪼개지는 context fragmentation 문제가 발생됨.

또한, evaluation 단계에서 고정된 segment를 보고 다음 token을 예측하게 되므로, 중복된 연산을 계속 수행하여서 토큰을 생성하는 문제도 있음.

Segment-Level Recurrence with State Reuse

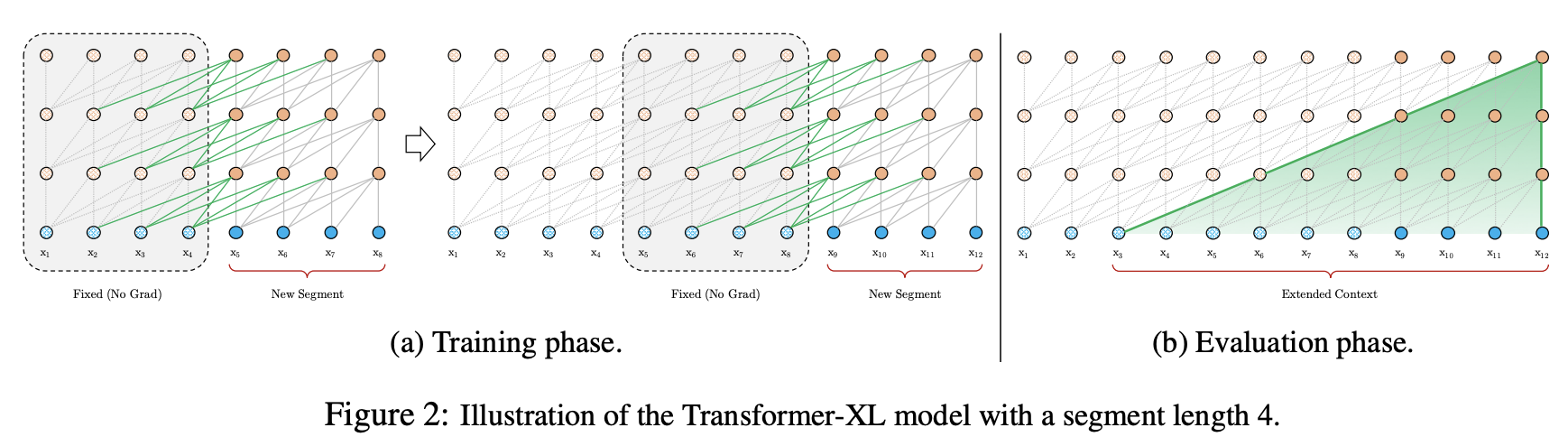
fixed-length context 문제를 해결하기 위해서 Transformer 구조에 Recurrence Mechanism을 사용함(Segment Recurrence).

앞선 segment에서 계산된 hidden state sequence 를 고정하고 캐싱하여 다음 seqment를 계산하는데 재사용함.

즉, 다음 segment의 첫번째 토큰에 대하여 예측을 할때, 이전 segment 모델의 캐싱된 결과를 사용함으로써 모델을 확장해나감.

이러한 Recurrence Mechanism을 사용함으로써, segment 사이에 long-term-dependency와 context fragmentation을 해결함.

수식적으로 보면 아래와 같음, 길이 L을 가진 Segment \(S\)

\[S_\tau = [x_{\tau,1,}...,x_{\tau,L}],\ S_{\tau+1} = [x_{\tau+1,1,}...,x_{\tau+1,L}] \notag\] \[\bar{h}^{n-1}_{\tau+1} = [SG(h^{n-1}_\tau) \circ h^{n-1}_{\tau+1}], \\ q^{n}_{\tau+1}, k^{n}_{\tau+1}, v^{n}_{\tau+1} = h^{n-1}_{\tau+1}W^{\top}_q, \bar{h}^{n-1}_{\tau+1}W^{\top}_k, \bar{h}^{n-1}_{\tau+1}W^{\top}_v, \\ h^{n}_{\tau+1} = Transformer-Layer(q^n_{\tau+1}, k^n_{\tau+1}, v^n_{\tau+1}) \notag\]

SG는 여기서 stop-gradient를 의미, \([SG(h^{n-1}_\tau) \circ h^{n-1}_{\tau+1}]\) 는 concatencation을 의미, \(W\)는 모델 파라미터

기존 Vanilla Transformer와 달리 attention의 key, value는 현재 segment 내 이전 layer의 값만 사용하는 것이 아닌, 이전 segment의 layer 값을 concat 하여 연산에 사용하게 됨.

이것을 반복하게 되면 넓은 receptive field와 segment에서 정보를 가져올 수 있게 됨.

또한, 바닐라와 비교하여 빠른 evaluation이 가능함. 이전 segment에서 계산된 값을 캐싱하여 재사용할 수 있으므로, GPU 메모리 한도까지 이전 segments를 캐싱하여서 사용할 수 있음.

Relative Positional Encodings

Transformer-xl은 segment 단위로 transformer 모델을 inference하면서, 이전 segment의 계산 결과를 캐싱해서 다음 모델에서 사용을 하고 토큰에 대하여 예측을 할때, 이전 inference 의 캐싱된 결과를 사용함으로써 모델을 확장함

여기서 기존 positional Encoding에 대하여 문제가 생기는데, segment에서 절대적인 위치로 위치정보를 주는 기존 방법에서는 segment1에서 첫번째 토큰이랑 segment2에서 첫번째 토큰이랑 같은 positional information을 가지는 문제가 발생됨.

Transformer-xl은 이러한 문제를 해결하기 위해서 기존 absolute positional encoding이 아닌 key랑 query 벡터 사이의 상대적인 위치를 이용한 relative positional encoding을 도입함.

positional encodings : \(U \in \mathbb{R}^{Lmax \times d}\), \(U_i\)는 i번째 absolute positional encoding, \(Lmax\)는 모델의 max 길이

positional encoding을 recurrence 모델에 적용하면 아래와 같아짐

\[h_{τ+1}=f(h_τ,E_{s_{τ+1}}+U_{1:L}) \\ h_τ=f(h_{τ−1},E_{s_τ}+U_{1:L}) \notag\]

\(E_{s_\tau}\)는 sequence \(s_\tau\)의 word embedding.

위에서 문제는 다른 word인 \(E_{s_\tau}, E_{s_{\tau+1}}\)가 같은 positional encoding 값을 가지게 되고, 모델은 각 segment 마다 같은 위치에 들어오는 token에 대하여 구분을 할 수 없게 되는 문제점이 발생하게 됨.

기존 Absolute Positional Encoding을 이용한 Query q와 Key k 사이에 attention(\(Q^{\top}K\)) 은 \(W_q(E_{x_i} + U_i)^{\top}(W_k(E_{x_j} + U_j))\) 이고 수식을 전개하면 아래와 같음.

\[\begin{aligned} \textbf{A}_{ij}^{abs} ={} \underbrace{\textbf{E}_{x_i}^{\top} \textbf{W}_q^{\top} \textbf{W}_k \textbf{E}_{x_j}}_{(a)} + \underbrace{\textbf{E}_{x_i}^{\top} \textbf{W}_q^{\top} \textbf{W}_k \textbf{U}_{j}}_{(b)} + \underbrace{\textbf{U}_{i}^{\top} \textbf{W}_q^{\top} \textbf{W}_k \textbf{E}_{x_j}}_{(c)} + \underbrace{\textbf{U}_{i}^{\top} \textbf{W}_q^{\top} \textbf{W}_k \textbf{U}_{j}}_{(d)} \end{aligned} \notag\]

여기서 몇가지를 바꾸어서 Relative Positional Encoding을 만듬.

\[\begin{aligned} \textbf{A}_{ij}^{rel} ={}\underbrace{\textbf{E}_{x_i}^{\top} \textbf{W}_q^{\top} \textbf{W}_{k,E} \textbf{E}_{x_j}}_{(a)} +\ \underbrace{\textbf{E}_{x_i}^{\top} \textbf{W}_q^{\top} \textbf{W}_{k,R} \color{blue}{\textbf{R}_{i-j}}}_{(b)} \\ +\ \underbrace{\color{red}{u^{\top}} \textbf{W}_{k,E} \textbf{E}_{x_j}}_{(c)} +\ \underbrace{\color{red}{v^{\top}} \textbf{W}_{k,R} \color{blue}{\textbf{R}_{i-j}}}_{(d)} \end{aligned} \notag\]

• term (b), (d)에 있던 absolute positional embedding \(U_j\)를 relative counterpart \(\color{blue}{R_{i-j}}\)로 변경
  • R은 기존 Transformer 에서 사용하던, sinusoid encoding matrix를 사용
• 학습가능한 파라미터인 \(\color{red}{u} \in \mathbb{R}^d\), \(\color{red}{v} \in \mathbb{R}^d\) 를 도입
  • \(q_i\) 를 기준으로 \(k_j\) 와의 관계를 찾는 것에서 모든 쿼리 위치에 대하여 동일하므로, 다른 위치에서도 같은 attentive bias를 가지고 위하여 도입
• \(W_{k,E}, W_{k,R}\) context-based key vector와 location-based key 벡터를 생성하기 위해서 파라미터를 분리

논문에서는 각 텀이 의미하는 내용이 아래와 같다고 주장

• term (a) : represents context based addressing

  • 문맥을​ 표현한다라.. -> 이건 ㅇㅇ

• term (b) : captures a content dependent positional bias

  • 콘텐츠의 의존적인 positonal bias 라…. 어떤 거지? -> 질의 토큰과 상대적인 위치에 토큰들?

• term (c) : governs a global content bias

  • global 콘텐츠의 bias? -> 모든 key 토큰에 대하여 bias 값?

• term (d) : encodes a global positional bias

  • global positional bias를 인코딩?? -> 모든 positional bias 대한 값?

최종적인 Transformer-XL architecture.

\[\bar{h}^{n-1}_\tau = [SG(m_{\tau}^{n-1} \circ h^{n-1}_\tau)] \\ q^n_\tau,k^n_\tau,v^n_\tau = h^{n-1}_\tau {W^n_q}^\top, \bar{h}^{n-1}_\tau {W^n_{k,E}}^\top, \bar{h}^{n-1}_\tau {W ^n_v}^\top \\ A^{n}_{\tau, i,j} = {q^n_{\tau, i}}^\top k^n_{\tau,j} + {q^n_{\tau,i}}^\top W^n_{k, R}R_{i-j} + {u}^\top k_{\tau,j} + v^\top W^n_{k, R}R_{i-j} \notag\]

\[\mathbb{a}^n_\tau = Masked-Softmax(A^n_\tau)\mathbb{v}^n_\tau \\ \mathbb{o}^n_\tau = LayerNorm(Linear(\mathbb{a}^b_\tau) + h^{n-1}_\tau) \\ h^n_\tau = Positionwise-Feed-Forward(\mathbb{o}^n_\tau) \notag\]

이전 segment와 concat한 결과를 이용해 \(q,k,v\) 를 만들고 attention score를 만들어냄.

첫번째, Segment는 초기 입력으로 \(h^0_\tau := E_{s_\tau}\), word_embedding이 c초기값을 들어감.

Experiments

Main Results

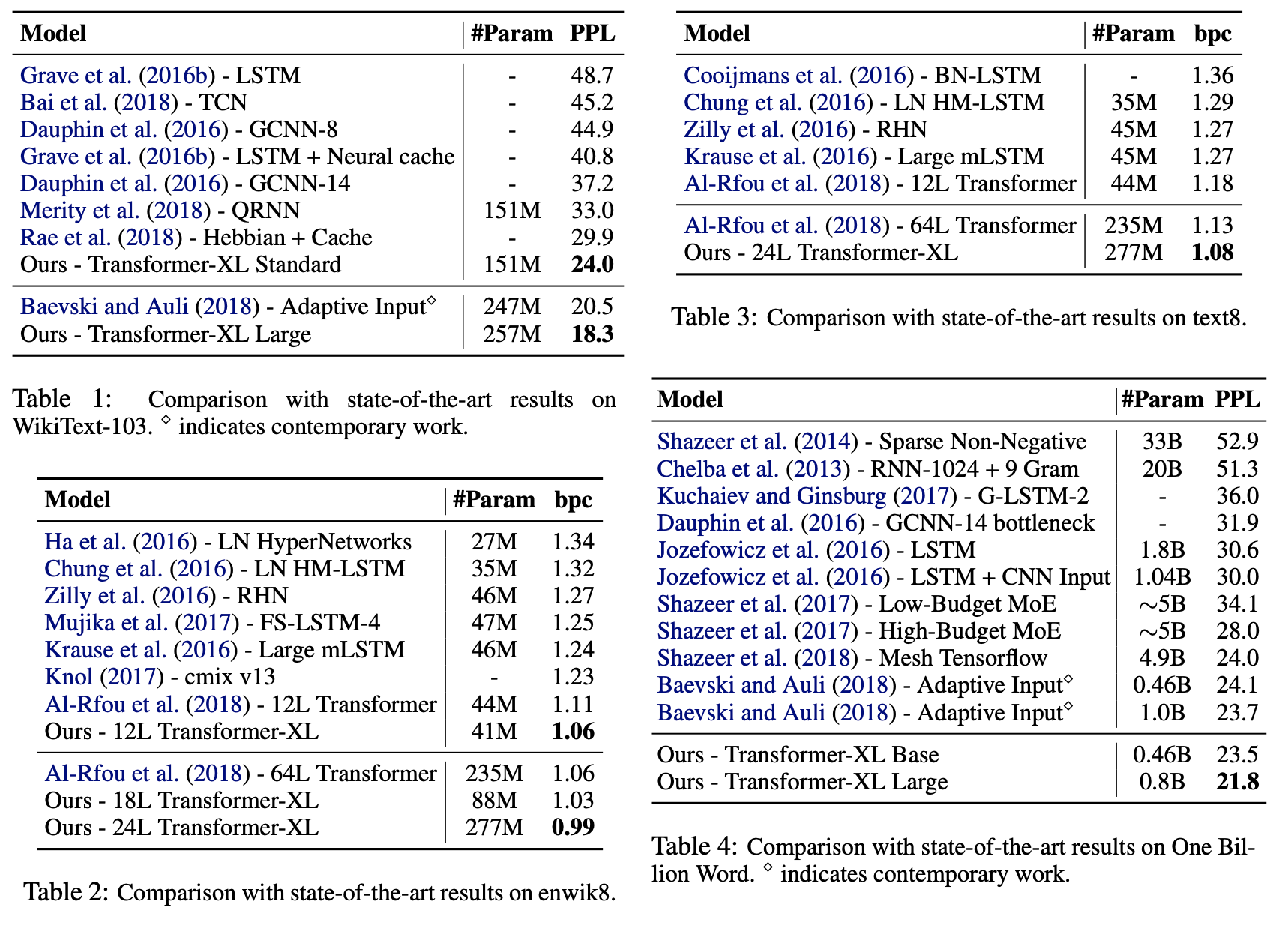
Ablation Study

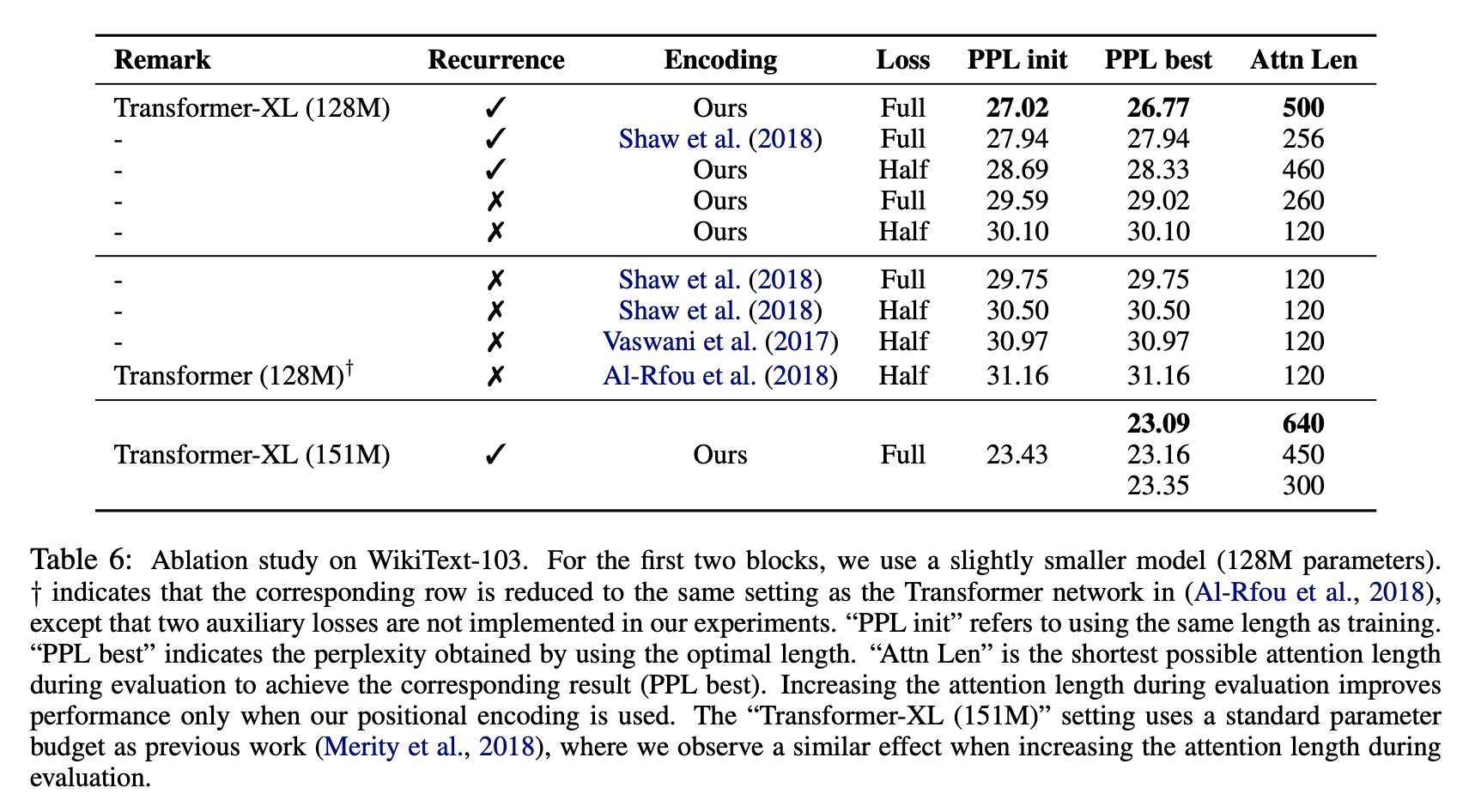
Relative Effective Context Length

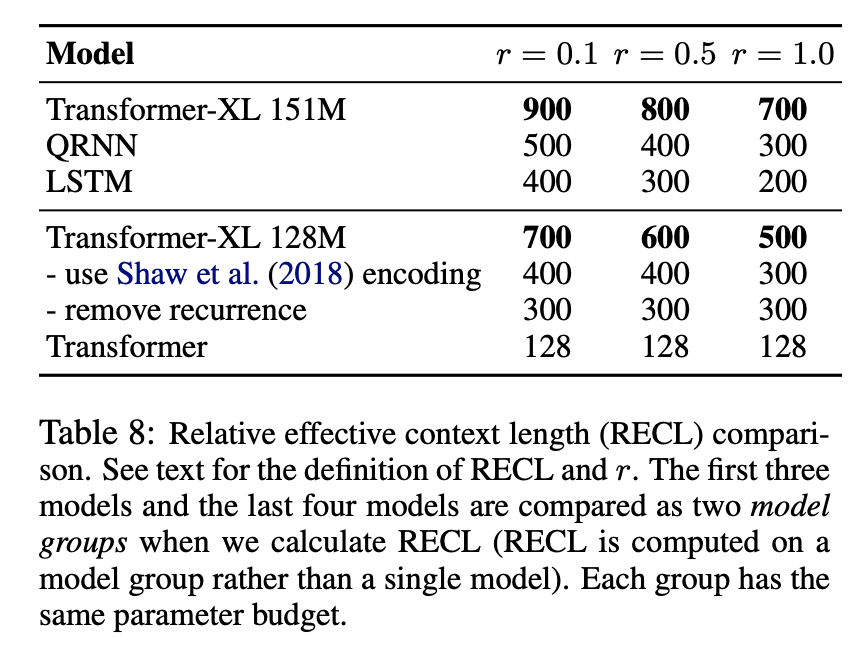
• Relative Effective Context Length (RECL)를 제안, 기존 Effective Context Length(ECL)의 문제점을 개선

Generated Text

Evaluation Speed