Attention Augmented Convolutional Networks

Paper link : https://arxiv.org/pdf/1904.09925.pdf, iccv 2019

요약

• google에서 iccv 2019에서 발표한 논문
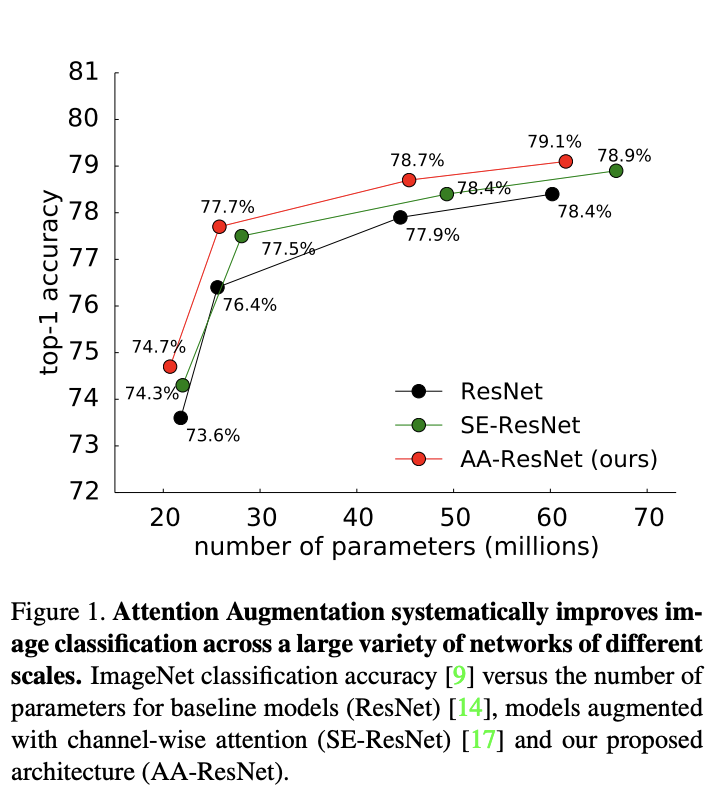
• convolutional layer와 self-attention을 결합한 새로운 방법을 제안하여 resnet에서 더 작은 파라미터로 top class에 대한 classification에서 이기는 결과를 얻음
• Transformer의 self-attention 구조를 비전 태스크에 맞도록 사용함

self-attention은 long range interaction을 캡처 하기 위해 서 최근에 사용되었지만, 대부분 시퀀스 또는 생성 모델에서만 사용 되었음. self-attention의 주요 아이디어는 히든 유닛으로 부터 가중치된 평균 값을 생성한다는 것, pooling과 conv 달리 가중치된 평균 연산에서 생성되는 가중치는 히든유닛 사이에 similarity function을 통해서 동적으로 생성됨

결과적으로 input signal 간의 상호작용은 conv 처럼 상대적인 위치에 의해 미리 결정되는 것이 아니라 신호자체에 의존됨.

특히 이것은 self-attention이 매개변수를 늘리지 않고도 long range interaction을 포착할 수 있도록 함.

Related Work - Self-Attention

논문에서 이미지에 대한 Self Attention 식이 Transformer에 Self Attention과 유사함.

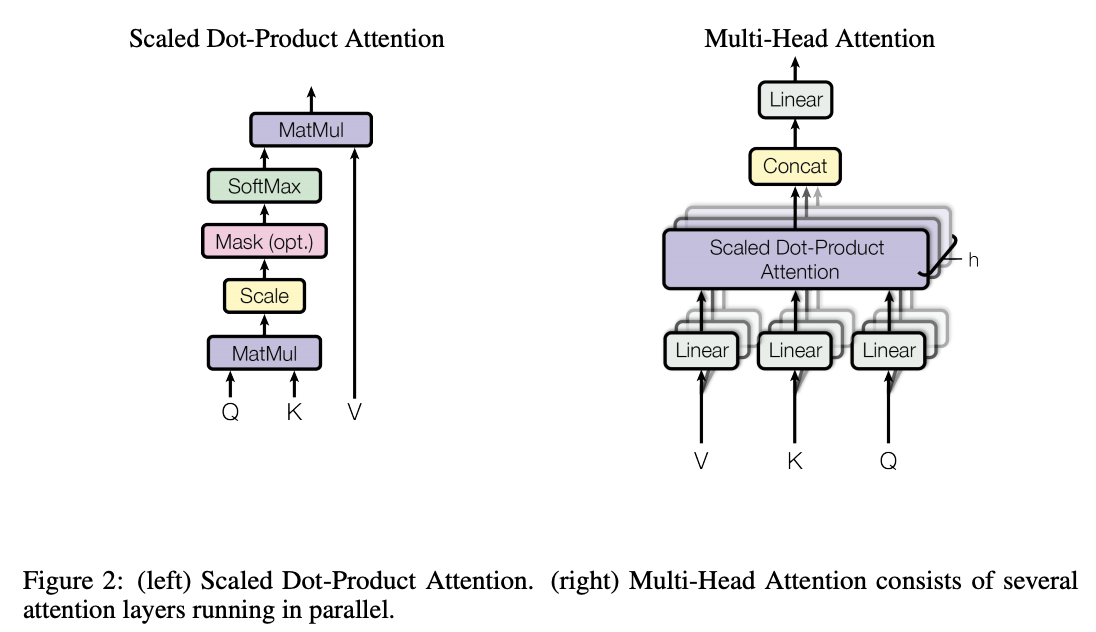
Transformer (Multi-Headed Self-Attention)

트랜스포머는 encoder와 decoder 구조로 이루어진 machine translation에서 first SOTA 결과를 보여준 architecture이다.

RNN에서처럼 하나하나 token을 받아서 처리하는 방식이 아닌 전체 token을 받고, attention module은 query, key, value의 학습되는 weight를 베이스로 token들 사이에 dependency를 학습함.

트랜스포머에서는 token의 위치적인 정보를 주기 위해서 Positional Encoding이라는 것을 추가하여 모델이 위치적인 정보를 학습할 수 있도록 함

Transformer Attention Function

​ \(Attention(Q, K, V) = softmax({QK^T \over \sqrt{d_k}}) V\)

방법

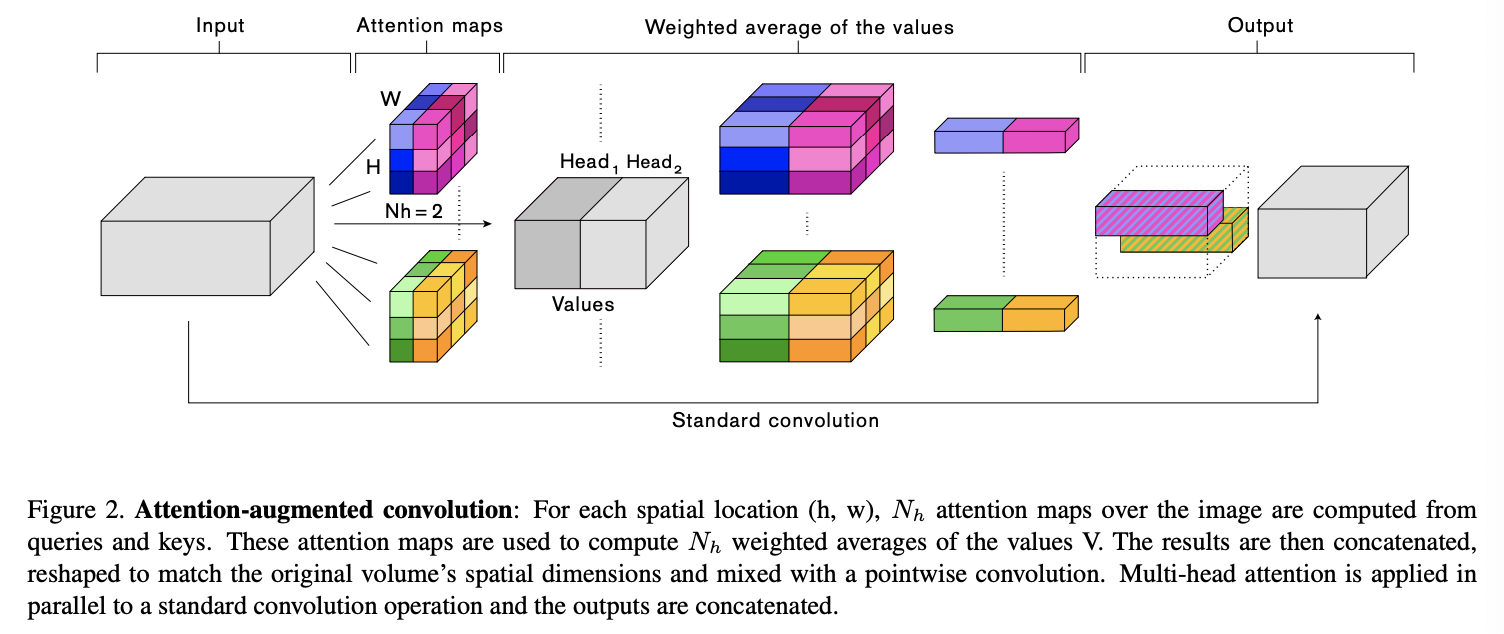
AACN은 MHA과 기존 convolution 연산과 같이 진행하여서 결과를 concat하는 방식으로 구현이 되어 있음 .

Self-Attention over images

batch 차원을 뺀 input tensor의 shape를 (H, W, F_in) 이라고 하면, 이걸 \(X \in \mathbb{R}^{HW \times F_{in}}\) 으로 flat하게 한 후 multihead attention을 적용할 수 있다.

이러한 self-attention의 output은 아래와 같이 나타 낼 수 있음 \(O_h = Softmax({(XW_q)(XW_k)^T \over \sqrt{d^h_k}})(XW_v)\) \(W_q\),\(W_k\),\(W_v\) 는 input X를 각각 Query(\(XW_q\)), Key(\(XW_k\)), Value(\(XW_v\))로 매핑하도록 학습이 된다.

이러한 모든 head 를 concat 하고 project 하면 아래와 같음. \(MHA(X) = Concat[O_1,...,O_{Nh}]W^o\) 가 되고 이를 reshape하여 \((H, W, d_v)\)의 shape 벡터를 생성할 수 있다.

Two-dimensional Positional Embedings

position 정보가 없다면 self-attention에서는 permutation equivariant 문제가 발생하게 됨. \(MHA(\pi(X)) = \pi(MHA(X))\) permutation equivariant 문제는 vision task에서 표현력을 제한 하는 문제가 됨.

논문에서는 이러한 문제를 완하하기 위해서 spatial information을 가지는 augument activation map의 multiple positional encoding을 사용함.

Image Transformer 논문에서는 sinusoidal wave를 2차원 input에 대하여 확장을 하였고

CoordConv는 positonal channels을 activation map에 concat 하였다.

하지만 이러한 encoding은 논문의 실험에서는 도움이 되지 못했음

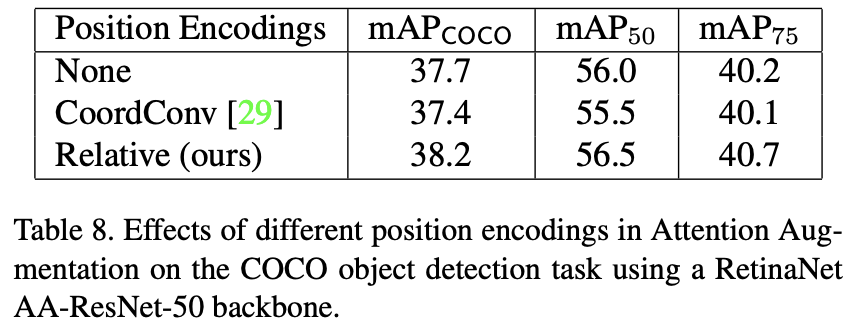
(Section 4.5)

논문에서는 이러한 positional encoding은 permuation equivariant 하지 않지만, 이미지를 다룰 때 바람직한 속성의 translation equivariance를 만족하지 않기 때문이라고 가설함.

논문에서는 relative position encoding을 확장한 방법을 제안함.

translation equivariance란 입력의 위치가 변하더라도, 영향을 받지 않아야 하는 것, 이미지의 stationarity 특성을 만족해야하는 뜻인듯 함.

Relative positional embeddings:

relative postional embedding은 해당 논문에서 언어 모델링을 위하여 소개되어졌다.

relative attention \(y_{i,j} = \sum_{a,b \in \mathcal{N}_k(i,j)} (q_{ij}^{T}k_{ab} + q_{ij}^{T}r_{a-i, b-j}) v_{ab}\) row, col offset 은 뒤에 식의 형태로 concat이 되어서 embedding됨

앞 term : 쿼리로 부터의 요소의 내용을 의미

뒤 term : 쿼리로부터의 요소의 상대 거리를 의미

위 논문에서는 pixel \(i = (i_x, i_y)\), \(j = (j_x, j_y)\) 라고 할 때, attention logit은 아래와 같이 계산 가능하다. \(l_{i,j} = {q^T_i \over \sqrt{d^h_k}}(k_j + r^W_{j_x\ -\ i_x} + r^H_{j_y\ -\ i_y})\) \(q_i\)는 픽셀 i에 대한 query 벡터

\(k_j\)는 픽셀 j에 대한 key 벡터

\(r^W_{j_x - i_x}\), \(r^H_{j_y - i_y}\) 는 각각 가로, 세로의 상대적인 거리 차를 위해서 학습된 임베딩 벡터

\(\sqrt {d_k^h}\)는 rescaling을 위해서 추가된 term, \(d_k^h = d_k / N_h\)

head h에 대한 output은 아래와 같다. \(O_h = Softmax({QK^T + S^{rel}_H + S^{rel}_W \over \sqrt{d^h_k}})V\) \(S^{rel}_H,\ S^{rel}_W\ \in \mathbb{R}^{HW \times WH}\) 은 relative position 메트릭이고 가로와 세로 차원에 대하여, \(S^{rel}_H[i,j] = q^T_ir^H_{j_y-i_y},\ \ S^{rel}_W[i,j] = q^T_ir^W_{j_x-i_x}\)로 표현됨.

Attention Augmented Convolution

기존 방법들(SENet, BAM, CBAM)등 방식에서는 channel-wise만 고려되든지, channels과 spatial이 각각 고려되어서 feature map을 recalibrating 하므로서 long-range dependencies를 캡처 했다.

논문은

1. spatial과 feature subspace가 함께 집중될 수 있도록 하는 attention mechanism을 사용하였고
2. feature map을 refine하기 보다는 추가하는 걸 소개했다.

fig 2.에서 제안된 augmented convolution을 요약함.

concateneating convolutional and attentional feature maps:

\[AAConv(X) = Concat[Conv(X), MHA(X)].\]

AACONV는 Original Conv와 Attention Head를 concat하므로 최종 conv를 마늘어 낸다.

여기서 \(v = {d_v \over F_{out}}\)는 원래 아웃풋 필터 대비, attention channel의 비율이고, \(k = {d_k \over F_{out}}\)는 원래 출력 필터 대비 key의 깊이 비율이다.

Experiments

ResNets, MnasNet에서 CIFAR-100, ImageNet, COCO 데이터를 이용해서 실험.

image classification과 object detection task에 대하여 성능 향상이 있는지 체크.

convolution을 AA로 대체하여서 baseline과 비교 실험을 진행함.

CIFAR-100 image classification

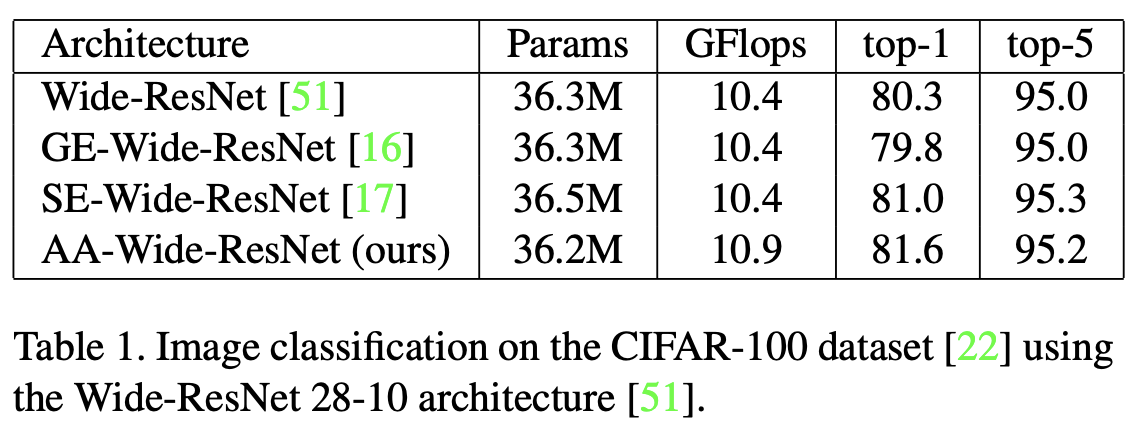
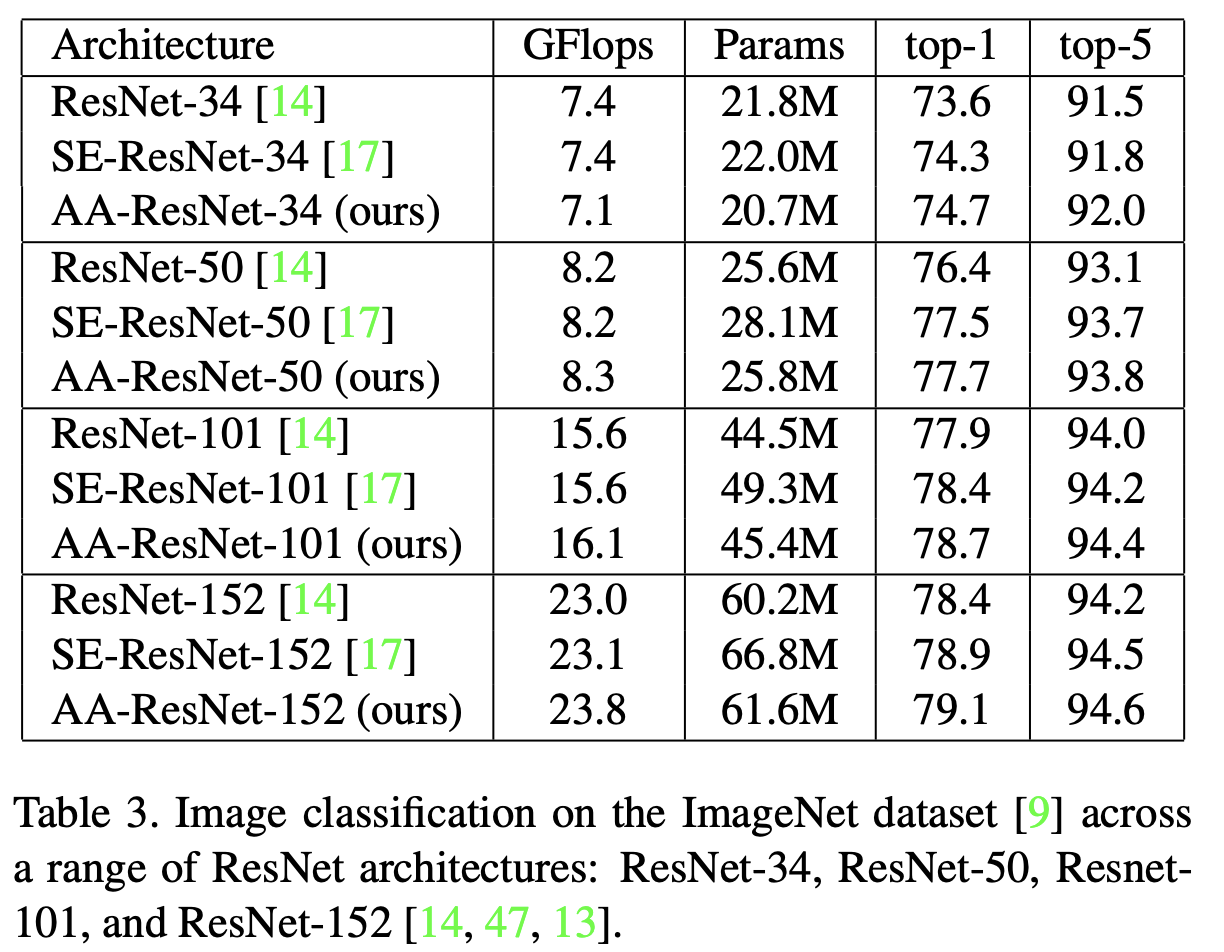
ImageNet image classification with ResNet

Ablation Study

Fully-attentional vision models:

모델의 파라미터인 k,v에 대하여 Ablation Study를 진행.

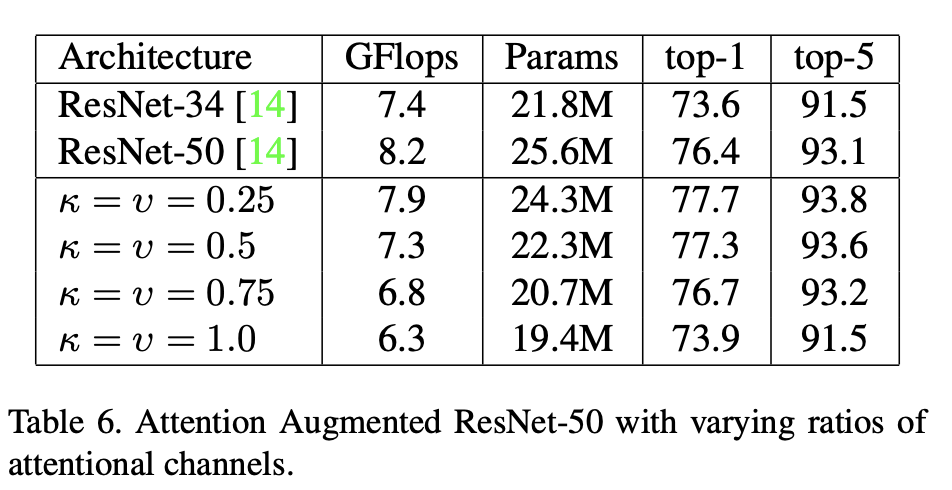
여기서 attention conv만 사용했을 때(k=v=1.0), 파라미터는 약 25% 줄었지만 성능은 약 2.5% 줄어들었고, 비슷한 성능을ResNet-34 보다 적은 파라미터로 달성함.

Importance of position encodings

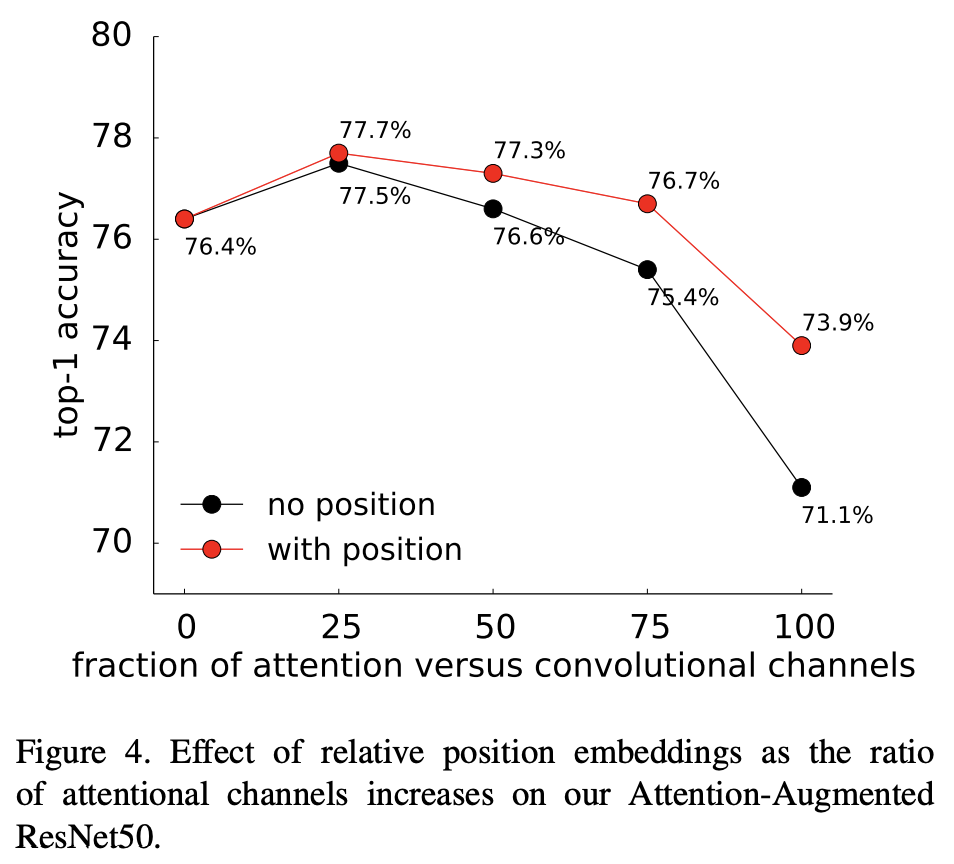
positional encoding의 중요점에 대하여, attention 채널의 비율을 높여가면서, 성능의 변화에 대하여 나타낸 그래프.

positional encoding을 하는 것이 성능이 더 좋았음을 보임.

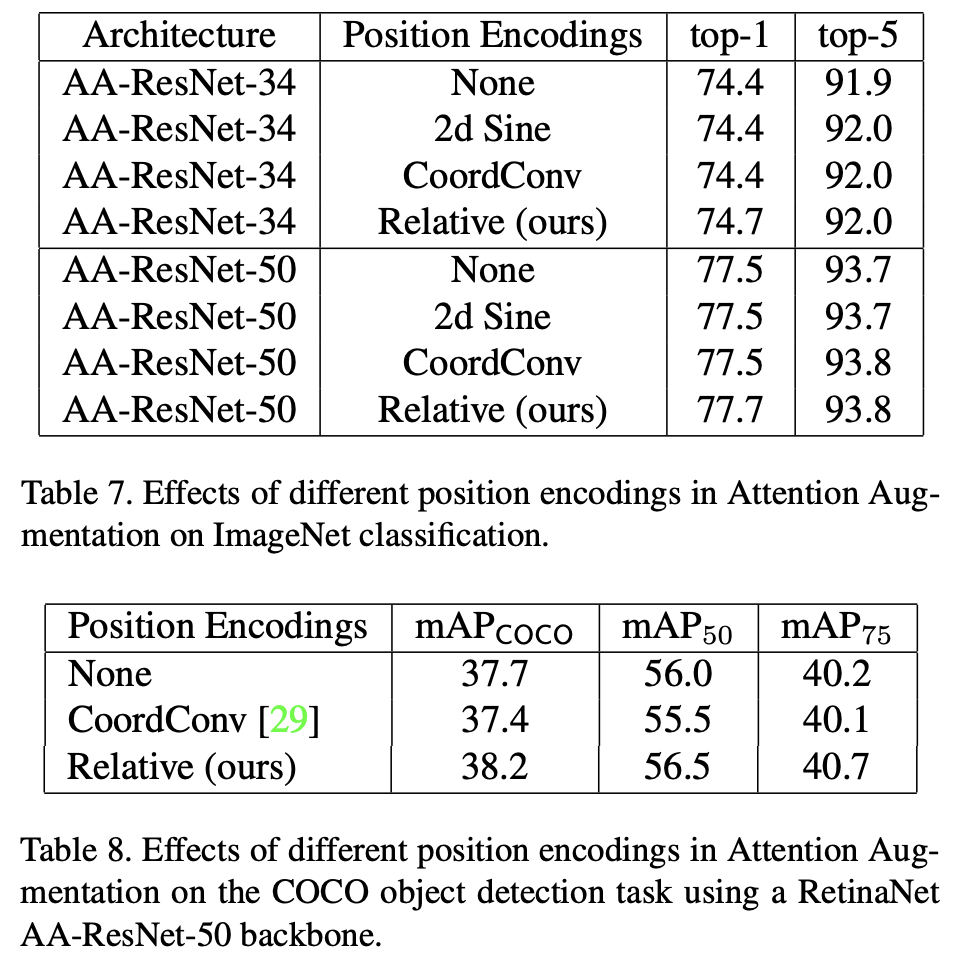
positional encoding 방식에 따른, 성능 차를 측정. 기존 다른 encoding 방법보다 relative encoding이 성능이 좋음을 보임.